深度学习中的常用音频处理方法
在利用深度学习给音乐打标签的实践过程中,我们不会把音频的原始信号直接作为模型的直接输入。常见的做法是我们会对音频信号做一系列的处理生成频谱图,而这里的频谱图常常是梅尔频谱或者是 MFCC, 这样处理得到的频谱图就是音频的“快照”。这样的快照才适合作为深度学习模型的输入。在这篇文章里我们就介绍一下这些音频处理提取特征的基本原理。
声音信号
声音是空气压力的变化产生的,声音信号则代表着空气压力随时间的变化。 声音信号通常以规律性的间隔重复,以使每个波具有相同的形状。 高度表示声音的强度,我们称其为振幅。 信号完成一个完整波所花费的时间叫周期,信号在一秒钟内产生的波数称为频率。 频率是周期的倒数,频率单位是赫兹。 我们遇到的大多数声音都可能不遵循这种简单而有规律的周期性模式。 但是可以将不同频率的信号加在一起,以创建具有更复杂重复模式的复合信号。 我们听到的所有声音(包括我们自己的声音)都包含此类波形

上面的波形图展示的是声音信号在时域的表示。与之相对的就是信号在频域的表示,即自变量是频率,即横轴是频率,纵轴是该频率信号的幅度(振幅)。
时域图:表现的是一段音频在一段时间内音量的变化,波形实质上是将各个频率的波形叠加在了一起(波形是由各频率不同幅值和相位的简单正弦波复合叠加得到的。
频谱图:表现的是一段音频在某一时刻各个频率的音量的高低,表示的是一个静态的时间点上各频率正弦波的幅值大小的分布状况 (各个时刻是一样的,即与时间无关)
下图展示了正弦波声音信号的时域到频域的转换

频谱生成
通信相关专业同学都知道信号的频谱就是用傅里叶变换算出来的。而在数字世界中我们必须把连续信号经过采样变成离散信号,所以对离散信号的频谱计算就是我们常说的离散傅里叶变换(DFT)。那为什么后来又有个快速傅里叶变换(FFT) 呢?从名字我们就知道就是 FFT 就是 DFT 的时机复杂度优化版本。
但在实际的音频信号处理中用的都是短时傅里叶变换(STFT, Short Time Fourier Transform)。为什么要用 STFT 呢?
自然界中几乎所有信号都是非平稳信号(信号的频率特性在任何时间会发生改变),比如语音信号就是典型的非平稳信号。
通常傅里叶变换只适合处理平稳信号,对于非平稳信号,由于频率特性会随时间变化,为了捕获这一时变特性,我们需要对信号进行时频分析,就包括 STFT。例如在一段时间内,有很多信号先后出现后消失,直接做 DFT 无法判断出不同信号出现的先后顺序,而 STFT 通过每次取出信号中的一小段加窗后做 DFT 来反映信号随时间的变化。
做STFT时每次取出的一段信号,叫做一帧(frame)。每两帧之间的间隔为Hop Size,一般为frame长度的25%-75%。将对每一帧做DFT得到的结果拼接到一起,可以得到spectrogram。增加frame的长度,频域的信息会越准确。
下图非常生动的展示了信号的 STFT 过程。
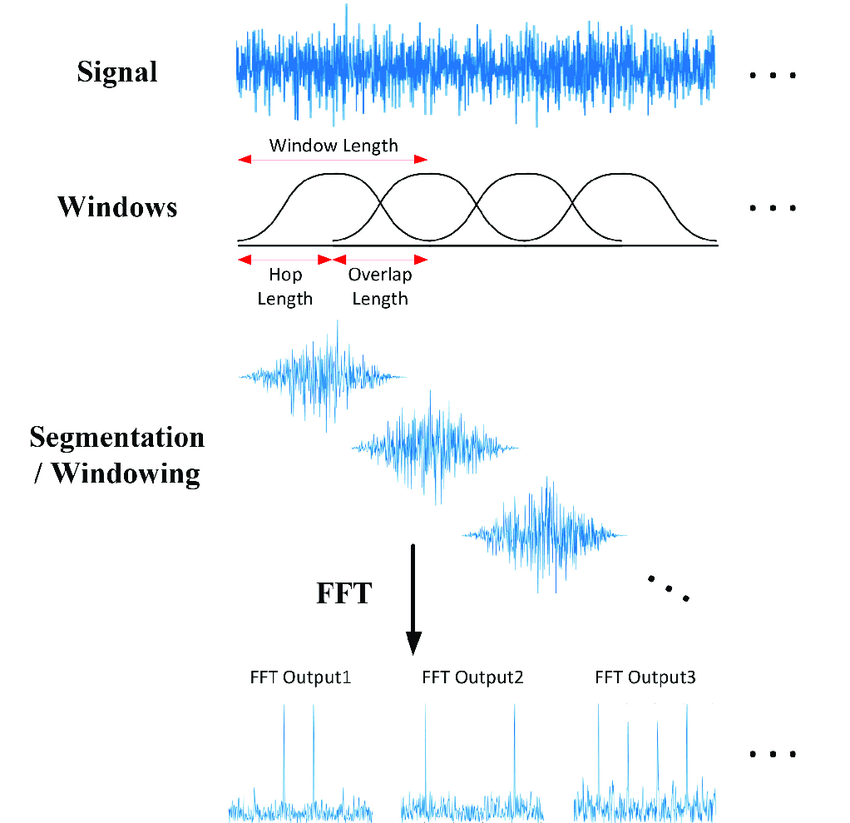
梅尔频谱(mel spectrum)
我们听到声音频率的方式称为“音调”,这是频率的主观印象。因此,高音调的声音比低音调声音的频率更大。人类不会线性感知频率,我们对低频之间的差异比高频更为敏感。我们可以轻松分辨出 500Hz和 1000Hz 之间的差异,但是即使两对之间的距离相同,我们也很难分辨出 10000Hz 和 10500Hz 之间的差异。
这时,梅尔标度(Mel Scale)被提出,它是Hz的非线性变换,表示人耳对等距音高(pitch)变化的感官,基于频率定义。
梅尔刻度与线性的频率刻度赫兹(Hz)之间可以进行近似的数学换算。一个常用的将 f 赫兹转换为m 梅尔的公式是:
m = 2595*log(1 + (f/700))
其参考点定义是将 1000Hz,且高于人耳听阈值 40 分贝以上的声音信号,定为 1000mel。在频率 500Hz 以上时,人耳每感觉到等量的音高变化,所需要的频率变化随频率增加而愈来愈大。这样的结果是,在赫兹刻度 500Hz 往上的四个八度(一个八度即为两倍的频率),只对应梅尔刻度上的两个八度。Mel 的名字来源于单词 melody,表示这个刻度是基于音高比较而创造的。

人类对声音振幅的感知就是声音的响度。与频率相似,我们听到的音量增大,一般都是非线性放大,而不是线性的,并且使用分贝表对此进行说明。 在此等级上,0dB 是完全静音。从此处开始,测量单位呈指数增长。10dB 是 0dB 的10倍,20dB是 100倍,30dB是 1000倍。在此规模上,高于 100dB 的声音开始变得让人难以忍受。 我们可以看到,为了以真实的方式处理声音,我们在处理数据的频率和幅度时,必须通过梅尔标度和分贝标度使用对数标度来转换频谱,这样转换后的频谱就称之为梅尔频谱。
梅尔倒谱系数(Mel-Frequency Cepstral Coefficients)
梅尔频谱图对于大多数音视频深度学习应用程序来说效果都是不错的。但是,对于人类语音的问题(如自动语音识别 ASR), MFCC(梅尔频率倒谱系数)的效果有时会更好。我们这里简要介绍一下 MFCC。首先了解一下倒频谱。
即倒频谱(信号)是信号频谱取对数的傅里叶变换后的新频谱(信号),倒频谱方便提取、分析原频谱图上肉眼难以识别的周期性信号,能将原来频谱图上成族的边频带谱线简化为单根谱线,受传感器的测点位置及传输途径的影响小。
MFCC 即就是组成梅尔频率倒谱的系数,广泛被应用于语音识别中。
下图描述了 MFCC 的处理流程

关于傅里叶变换,倒频谱,MFCC 等我们没有深入介绍背后的数学原理和计算。感兴趣的可以搜索相关主题进一步学习。
信号处理
文章的前半部分我们介绍了语音信号的特征提取的一般原理和过程。现在我们看看在工程上我们如何去实现以上步骤,这里我们拿非常受欢迎的语音处理库 Python 中的 librosa 来作为示例。
波形图
|
|

频谱图
|
|
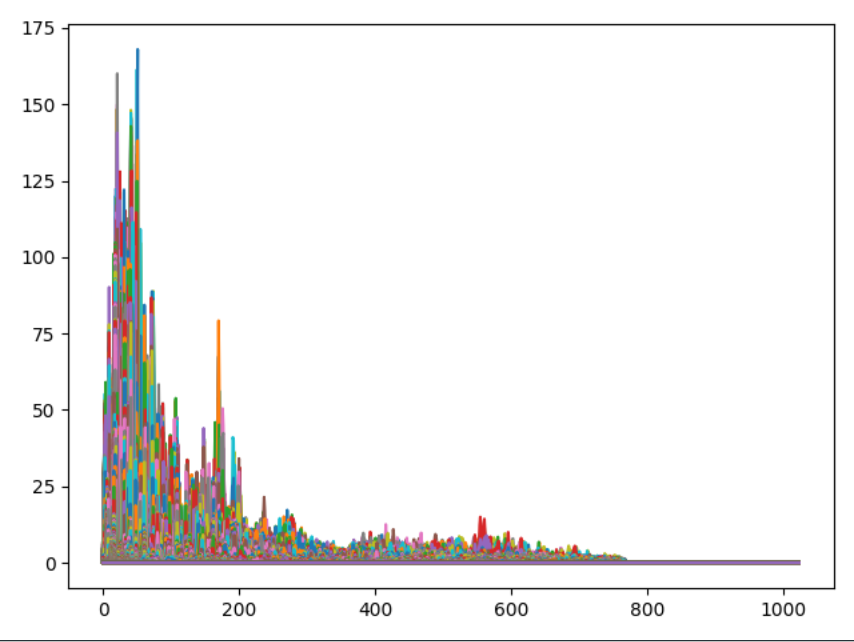
梅尔频谱图
|
|

MFCC
|
|

至此,在深度学习中对音频做预处理的基本原理就介绍完了,其中音频处理可能还包括的频谱图增强没有提及,感兴趣的同学可以继续研究。后续随着我们应用的深入可能会有文章继续介绍我们的一些实践。